H-Tyr(3-I)-OHCAS# 70-78-0 |
Quality Control & MSDS
3D structure
Package In Stock
Number of papers citing our products
| Cas No. | 70-78-0 | SDF | Download SDF |
| PubChem ID | 439744 | Appearance | Powder |
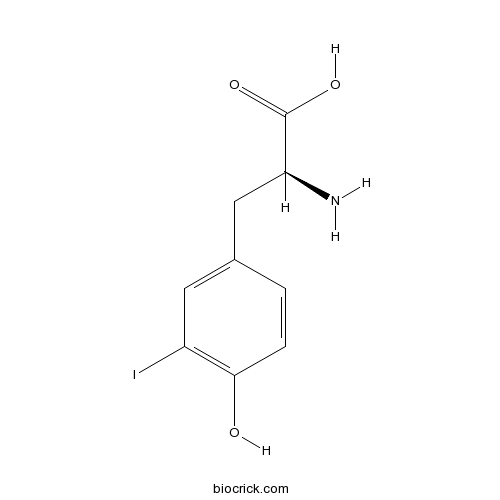
| Formula | C9H10INO3 | M.Wt | 307.1 |
| Type of Compound | N/A | Storage | Desiccate at -20°C |
| Synonyms | 3-Iodo-L-tyrosine; 70-78-0; H-Tyr(3-I)-OH; 3-IODO-TYROSINE | ||
| Solubility | H2O : 6.25 mg/mL (20.35 mM; Need ultrasonic) DMSO : < 1 mg/mL (insoluble or slightly soluble) | ||
| Chemical Name | (2S)-2-amino-3-(4-hydroxy-3-iodophenyl)propanoic acid | ||
| SMILES | C1=CC(=C(C=C1CC(C(=O)O)N)I)O | ||
| Standard InChIKey | UQTZMGFTRHFAAM-ZETCQYMHSA-N | ||
| Standard InChI | InChI=1S/C9H10INO3/c10-6-3-5(1-2-8(6)12)4-7(11)9(13)14/h1-3,7,12H,4,11H2,(H,13,14)/t7-/m0/s1 | ||
| General tips | For obtaining a higher solubility , please warm the tube at 37 ℃ and shake it in the ultrasonic bath for a while.Stock solution can be stored below -20℃ for several months. We recommend that you prepare and use the solution on the same day. However, if the test schedule requires, the stock solutions can be prepared in advance, and the stock solution must be sealed and stored below -20℃. In general, the stock solution can be kept for several months. Before use, we recommend that you leave the vial at room temperature for at least an hour before opening it. |
||
| About Packaging | 1. The packaging of the product may be reversed during transportation, cause the high purity compounds to adhere to the neck or cap of the vial.Take the vail out of its packaging and shake gently until the compounds fall to the bottom of the vial. 2. For liquid products, please centrifuge at 500xg to gather the liquid to the bottom of the vial. 3. Try to avoid loss or contamination during the experiment. |
||
| Shipping Condition | Packaging according to customer requirements(5mg, 10mg, 20mg and more). Ship via FedEx, DHL, UPS, EMS or other couriers with RT, or blue ice upon request. | ||

H-Tyr(3-I)-OH Dilution Calculator

H-Tyr(3-I)-OH Molarity Calculator
| 1 mg | 5 mg | 10 mg | 20 mg | 25 mg | |
| 1 mM | 3.2563 mL | 16.2813 mL | 32.5627 mL | 65.1254 mL | 81.4067 mL |
| 5 mM | 0.6513 mL | 3.2563 mL | 6.5125 mL | 13.0251 mL | 16.2813 mL |
| 10 mM | 0.3256 mL | 1.6281 mL | 3.2563 mL | 6.5125 mL | 8.1407 mL |
| 50 mM | 0.0651 mL | 0.3256 mL | 0.6513 mL | 1.3025 mL | 1.6281 mL |
| 100 mM | 0.0326 mL | 0.1628 mL | 0.3256 mL | 0.6513 mL | 0.8141 mL |
| * Note: If you are in the process of experiment, it's necessary to make the dilution ratios of the samples. The dilution data above is only for reference. Normally, it's can get a better solubility within lower of Concentrations. | |||||

Calcutta University

University of Minnesota

University of Maryland School of Medicine

University of Illinois at Chicago

The Ohio State University

University of Zurich

Harvard University

Colorado State University

Auburn University

Yale University

Worcester Polytechnic Institute

Washington State University

Stanford University

University of Leipzig

Universidade da Beira Interior

The Institute of Cancer Research

Heidelberg University

University of Amsterdam

University of Auckland

TsingHua University

The University of Michigan

Miami University

DRURY University

Jilin University

Fudan University

Wuhan University

Sun Yat-sen University

Universite de Paris

Deemed University

Auckland University

The University of Tokyo

Korea University
H-Tyr(3-I)-OH
- 1-(4-Hydroxyphenyl)propan-1-one
Catalog No.:BCN4597
CAS No.:70-70-2
- H-Asn-OH
Catalog No.:BCC2875
CAS No.:70-47-3
- L-Glutathione Reduced
Catalog No.:BCC8030
CAS No.:70-18-8
- Triflurdine (Viroptic)
Catalog No.:BCC3873
CAS No.:70-00-8
- Isocostic acid
Catalog No.:BCN4260
CAS No.:69978-82-1
- 20(S),24(R)-Ocotillol
Catalog No.:BCN3891
CAS No.:69926-31-4
- Swertisin
Catalog No.:BCN2762
CAS No.:6991-10-2
- Cyanopindolol hemifumarate
Catalog No.:BCC6880
CAS No.:69906-86-1
- Cinalbicol
Catalog No.:BCN7464
CAS No.:69904-85-4
- Immethridine dihydrobromide
Catalog No.:BCC7328
CAS No.:699020-93-4
- Rhapontisterone B
Catalog No.:BCN2664
CAS No.:698975-64-3
- (+)-Isoajmaline
Catalog No.:BCN3425
CAS No.:6989-79-3
- Indole-3-carbinol
Catalog No.:BCC5318
CAS No.:700-06-1
- 2-Adamantanol
Catalog No.:BCN8479
CAS No.:700-57-2
- 2-Adamantanone
Catalog No.:BCN8473
CAS No.:700-58-3
- Terazosin HCl
Catalog No.:BCC4354
CAS No.:70024-40-7
- Rivularin
Catalog No.:BCN3189
CAS No.:70028-59-0
- LPYFD-NH2
Catalog No.:BCC6113
CAS No.:700361-48-4
- 4,10-Aromadendranediol
Catalog No.:BCN4261
CAS No.:70051-38-6
- Acronycine
Catalog No.:BCC8114
CAS No.:7008-42-6
- LY2109761
Catalog No.:BCC3806
CAS No.:700874-71-1
- LY2157299
Catalog No.:BCC3709
CAS No.:700874-72-2
- TCN 237 dihydrochloride
Catalog No.:BCC6111
CAS No.:700878-19-9
- 5-Heneicosylresorcinol
Catalog No.:BCN7630
CAS No.:70110-59-7
Radiosynthesis and in vivo evaluation of the pseudopeptide delta-opioid antagonist [(125)I]ITIPP(psi).[Pubmed:11395309]
Nucl Med Biol. 2001 May;28(4):375-81.
The radioiodinated tetrapeptide delta-opioid antagonist [(125)I]ITIPP(psi) [H-Tyr(3'I)-Ticpsi[CH2NH]Phe-Phe-OH] (Ki(delta) = 2.08 nM; Ki(micro)/Ki(delta) = 1280) has been synthesized and evaluated as a potential lung tumour imaging agent. [(125)I]ITIPP(psi) was obtained, via electrophilic iodination, in 46% yield (>44,000 MBq/micromol) from the parent TIPP(psi). The biodistribution of [(125)I]ITIPP(psi) in nu/nu mice bearing SCLC-SW210.5 xenographs revealed good uptake and prolonged retention of radioactivity in organs known to possess delta-opioid receptors. Metabolite analysis showed that [(125)I]ITIPP(psi) was largely unmetabolized at 25 min PI and blocking studies showed significant reduction of uptake of the tracer in the brain, liver, intestine and tumor indicating that the iodinated tetrapeptide binds to delta opioid receptors in vivo.
New theoretical methodology for elucidating the solution structure of peptides from NMR data. II. Free energy of dominant microstates of Leu-enkephalin and population-weighted average nuclear Overhauser effects intensities.[Pubmed:8679943]
Biopolymers. 1996 Jan;38(1):69-88.
A small linear peptide in solution may populate several stable states (called here microstates) in thermodynamic equilibrium; elucidating its dynamic three dimensional structure by multi- dimensional nmr is complex since the experimentally measured nuclear Overhauser effect intensities (NOEs) represent averages over the individual contributions. We propose a new methodology based on statistical mechanical considerations for analyzing nmr data of such peptides. In a previous paper (called paper I, H. Meirovitch et al. (1995) Journal of Physical Chemistry, 99, 4847-4854] we have developed theoretical methods for determining the contribution to the partition function Z of the most stable microstates, i.e. those that pertain to a given energy range above the global energy minimum (GEM). This relatively small set of dominant microstates provides the main contribution to medium- and long-range NOE intensities. In this work the individual populations and NOEs of the dominant microstates are determined, and then weighted averages are calculated and compared with experiment. Our methodology is applied to the pentapeptide Leu-enkephalin H-Tyr-Gly-Gly-Phe-Leu-OH, described by the potential energy function ECEPP. Twenty one significantly different energy minimized structures are first identified within the range of 2 kcal/mol above the GEM by an extensive conformational search; this range has been found in paper I to contribute 0.6 of Z. These structures then become "seeds" for Monte Carlo (MC) simulations designed to keep the molecule relatively close to its seed. Indeed, the MC samples (called MC microstates) illustrate what we define as intermediate chain flexibility; some dihedral angles remain in the vicinity of their seed value, while others visit the full range of [-180 degrees, 180 degrees]. The free energies of the MC microstates (which lead to the populations) are calculated by the local states method, which (unlike other techniques) can handle any chain flexibility. The NOE of MC microstate i is calculated as the average <1/r(3)>i(2), and an effective interatomic distance ri(eff) is defined as ri(eff) =


